History

Concerning the history and background to parquet deformation of the William Huff model1 (all further references to the 'Huff model' here are based on this description), this is not a straightforward task to document as there are certain grey areas. Although there is indeed a 'big bang' moment, in 1960, by Peter Hotz/William Huff, there are indeed a few precursors, from as far back as 1886, some more tenuous than others, intended or otherwise, of which I document, on the grounds of including 'all', no matter how tenuous, given that there are so few. Indeed, some are so tenuous that others may disagree as to their inclusion. So be it. I would be very much indebted to anyone bringing to my attention any more, no matter how tenuous. The concept may very well appear in some obscure pattern/design book or other fields that are not necessarily well documented in the mathematical literature.

What is perhaps surprising to me though, is that no one had effectively thought of the concept before 1960. Despite many tiling studies, especially since the late 19th century, when the subject per se essentially took off, no one had apparently thought to have such a simple, and obvious, next-stage concept of a 'dynamic' tiling. And even after the 1960s 'true' beginning, it was still largely unknown, confined to obscure design journals, and certainly not the more likely field of mathematics. Only in 1983, with the publication of Douglas Hofstadter's article in the more mainstream Scientific American [*], did it attract popular and mathematical study. Since then, interest in the subject has exploded, in relative terms, with over 200+ practitioners, albeit this is still relatively low compared to the interest in tiling as such.

Note that this is very much an initial investigation, and like most of such investigations, will likely be improved upon a return after a period of reflection. Even with a first draft, it could still be improved further. However, the 'dreaded drift' is occurring, a term I use when my studies become effectively becalmed, and therefore I bring proceedings to a halt for now. Nonetheless, it remains an excellent piece. As far as I am aware, there is no previously written history of any kind in the field.

1 Defined by myself as a geometrical tiling metamorphosis, typically in 1-dimension as in a strip form, as an abstract entity (i.e. without any Escher-like element). Huff's definition, in Scientific American, is more restrictive, with conditions of handedness).

Contents

1. 1886, Lewis Foreman Day, forerunners in The Anatomy of Pattern
2. 1903, Lewis Foreman Day, forerunners in Pattern Design
3. 1917, D'Arcy Wentworth Thompson, first true parquet deformation, by accident or design
4. 1937+, Maurits Cornelis Escher (1), forerunners
5. 1960, Peter Hotz/William Huff, the first (1-dimensional) true parquet deformation, by intention
6. 1964, Arthur Carlson/Thomas C. Davies/David Oleson, the first 2-dimensional instance
7. 1965, William Huff, the first reference to parquet deformation in print
8. 1967-1968, Maurits Cornelis Escher (2), parquet deformation
9. 1968, William Huff, the first definition in print
10. 1983, Douglas Hofstadter, the first popular account in print
11. 2003+, Craig Kaplan, advanced concepts
12. 2015, Edmund Harriss, the first non-periodic (and incidentally 2-dimensional) parquet deformation

1. 1886, Lewis Foreman Day The Anatomy of Pattern (1)

Some early forerunners, perhaps generously stated (as others may disagree) of parquet deformation can be seen in the work of Lewis F. Day (1845–1910), a prominent exponent of the Arts and Crafts movement in the UK. However, it is not entirely clear what he is striving for. For certain, what we consider parquet deformation is not explicit, either in the diagrams or commentary. These appear in two books, in slightly different forms. The first appears in Text Books of Ornamental Design I, The Anatomy of Pattern, of 1887 [*] and the second Pattern Design, of 1904 [*], which repeats two of the diagrams, and of which for the sake of clarity I discuss each book individually.

Plate 11, of The Anatomy of Pattern shows two precursors to parquet deformation, with the upper of less connection than the lower. As the diagram was apparently drawn in 1886, I use this date rather than when the book was published, in 1897.

Upper, described by Day on the plate as 'zigzag' and 'wave' are somewhat tenuous, even within a generous definition of parquet deformation. A repeat zigzag line of a sharp angularity steadily progresses into a shallower wavy line. This (obviously) lacks a tiling element and so could easily (and fairly?) be summarily dismissed. However, as it is a rudimentary 'development' I have included it for interest's sake.

Lower, described by Day on the plate as (i) 'Wave-lines opposed' (ii) 'Joined to form ogee' and (iii) 'Inter-laced to form a net. An open repeat lattice based on ogee lines abruptly closes to form a tiling in the centre, of which this then again abruptly closes so the lines overlap. In effect, this is of three elements butted together; there is no smooth transformation. Prima facie, this is indeed of a better resemblance to the Huff model than the upper. But again, does this qualify as a parquet deformation? Cases for and against can be made. I am ambivalent about this. Day is not explicit in what he is doing. The commentary text in the book gives:

One may very easily deduce many of the common curvilinear patterns directly from angular motives. (Plate 11.) The wave, for example, is a zigzag, just blunted at the points. Soften the lines of the hexagon, and you have the ogee. Interlace straight rods, and you get waved lines, as may be seen in the perspective view of the common hurdle. Round the corners of the hexagon or octagon, and you arrive at a rude circle. The relation of the hexagon or octagon diaper to the diaper of circles is obvious. Presumably, the busy bee, if one may suggest such a thing without irreverence, only works in a circle, and the hexagonal form of the cells of the honeycomb is simply the result of gravitation; just as you find that cylinders crowded all become hexagonal prisms.

Metamorphosis, or development, is not mentioned. It could even be argued that he is simply concatenating his ideas as a single diagram. I am ambivalent overall on how to assess this.

Fig. 1. Plate 11. The Anatomy of Pattern 

2. 1903, Lewis Foreman Day

As is his wont, Day then reuses/modifies diagrams in earlier publications, of both the upper and lower The Anatomy of Pattern, in Pattern Design, to which he adds another diagram. Given that two of these are effectively the same as in The Anatomy of Pattern, I refer the reader to the commentary above, although for the sake of clarity, I show all three diagrams. The new diagram, p. 26, is captioned by Day, p. 26, 'Simple and More Complicated Trellis Lines', in a chapter on 'The Octagon'. Oddly, it is not discussed in the text! Again, it is by far from clear what Day is intended. The first half begins with a square tiling, then shows a series of overlapping squares, and then again overlapping rhombs. The transitions are abrupt. As such, best described as a forerunner 'of sorts'.

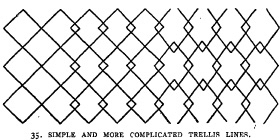
Fig. 2a. P. 26, Pattern Design. Simple and More Complicated Trellis Lines 

Fig. 2b. P. 27, Pattern Design. Zig-Zags developing into Wave Lines

Fig. 2c. P. 34, Pattern Design. Wave Lines, Ogee Diaper and Interlaced Ogees, Giving Hexagonal Shapes